ARC Drawing Algorithms
In the next part of our series on basic line drawing coding, we now look at arcs. We have done straight lines and circles, but how do we draw a bendy line or an arc?
We’ll probably run into our old friend Bresenham again in this section.
There are many ways to draw an arc, some more complex than others. The simplest algorithm is to calculate all the points on the boundary of the arc between the start and end angles and then draw the connecting lines between these points.
This algorithm although simple to code is quite slow and does not always generate smooth arcs.
For most general applications this method of arc generation is perfectly acceptable and is produced in only a few lines of code. The basic algorithm starts by calculating the start and end points of the arc and then working its way around the arc draws a line from the starting point to the next point found on the boundary. The continues in steps of x degrees until the final point is found and a line is drawn to the final arc endpoint.
One advantage of this technique is that it can be made faster by removing the number of steps between arc point coordinates. As we saw in the circle algorithm using around 72 points will give a fairly decent circle image. It is possible with this technique to limit the number of points whilst the initial arc is being drawn for speed and at a later stage to increase the number of points to draw a more accurate arc (but obviously much slower).
The basic arc algorithm can be implemented as follows.
//
//Basic Arc Algorithm
//
//Inputs
// X1,Y1 centre of Arc
// sa,ea start and end angles in degrees
// r radius of Arc.
//
//Definition of 1 degree in radian measure
#define degree_one 0.017453292
void Arc (float x1, float y1, float sa, float ea, float r)
{
float i;
float xs,ys,xe,ye;
xs= x1+r*cos(sa); //Calculate the start and end points of the Arc
ys= y1+r*sin(sa);
xe= x1+r*cos(ea);
ye= y1+r*sin(ea);
moveto(xs,ys);
for (i=sa; i<ea; i+="degree_one)" draw="" arc="" in="" steps="" of="" 1="" degree<br=""> {
lineto(x1+ (r*cos(i)) , y1+ (r*sin(i)) ); //Draw line to next arc point
}
lineto(xe,ye); //Close final arc line.
}</ea;>
The main disadvantage of this algorithm is its use of floating point math to calculate each point along the way. This can be very time consuming and should really be avoided. What we need is an Integer-based algorithm that is both fast and accurate. One of the fastest methods to draw arcs is based on the Bresenham circle algorithm. If you consider your circle to be broken into eight sectors then for any given arc all that is required is to calculate which sectors are drawn and then using the Circle algorithm plot only the correct points in those sectors.
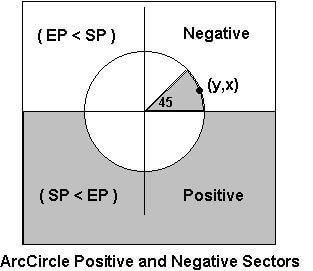
Using the circle algorithm we only need to calculate points for the first sector and then reflect those points into the other sectors for drawing. The only problem we have to overcome is to know what points are plotted in each sector. The easy bit is to start by working out which sectors are not drawn at all and then eliminate these from the plot routines. After this, we calculate which sectors are drawn completely and mark these to draw every point. The problem then occurs of working with partially drawn sectors. Due to the fact that these points are reflected in the circle’s center, it makes it difficult to calculate where on the arc these points lie. The algorithm I use is based on the Positive and negative direction of the arc drawing. If you take an arc starting a 0 degrees and ending at 45 you will see this arc will be drawn from right to left across the top of our circle as shown in the diagram below.
For every arc drawn along the top of the circle, the EndAngle Point will always be smaller than the StartAngle Point. Using this information as a basis we need only calculate if our selected X point will be between EP and SP before plotting it.
In the same way, we do the reverse for any points after 180 degrees as these points will be flowing in the positive direction, left to right. At first sight, this algorithm looks quite complex and is quite lengthy, but it compensates for this in speed and accuracy. It requires only 3 code modules, the basic circle algorithm, and code to handle the Positive and Negative sector areas. The algorithm only requires floating point math at the start to calculate the arc start and end points. With a little thought, the floating point lines could be calculated using integer math and increase the speed that little bit more.
//
//Arc Algorithm based on Bresenham Circle routine.
//
//Define variables for Arc sectors
//
#define NOT_DRAWN 0
#define STARTS_HERE 1
#define ALL_DRAWN 2
#define ENDS_HERE 3
#define STARTS_ENDS_HERE 4
//Radian to degree conversion value.
#define R_TO_D 57.29578
//===============================================================================
//Circle Sector flags
// Global access by all routines.
//===============================================================================
int arc_sector[8];
//===============================================================================
//FastArc
// Draw an arc,
// Inputs
// xc,yc Centre of arc
// sa,ea start and end angle in degrees
// r radius
//===============================================================================
void FastArc (int xc, int yc, int sa, int ea, int r)
{
int start_sector,end_sector;
int i;
int x,y;
int ep,sp,d;
//Clear all the arc sector flags,
for (i= 0; i< 8; i++)
arc_sector[i] = NOT_DRAWN;
//Calculate the start and end Arc sectors
start_sector = sa / 45;
end_sector = ea / 45;
if (start_sector == end_sector) {
arc_sector[start_sector] = STARTS_ENDS_HERE;
}
else {
for (i = start_sector; i< end_sector; i++) arc_sector[i] = ALL_DRAWN; arc_sector[start_sector] = STARTS_HERE; arc_sector[end_sector] = ENDS_HERE; } /*''Calculate the Start and End Points*/ /*''Calculate points in first sector and translate*/ x = 0; y = r; sp = ((double)xc + (double)r * cos((double)sa/R_TO_D)); ep = ((double)xc + (double)r * cos((double)ea/R_TO_D)); d = 2 * (1 - r); while (y > x)
{
NegativeSectorPoint(xc + y, yc + x, 0, sp, ep);
NegativeSectorPoint(xc + x, yc + y, 1, sp, ep);
NegativeSectorPoint(xc - x, yc + y, 2, sp, ep);
NegativeSectorPoint(xc - y, yc + x, 3, sp, ep);
PositiveSectorPoint(xc - y, yc - x, 4, sp, ep);
PositiveSectorPoint(xc - x, yc - y, 5, sp, ep);
PositiveSectorPoint(xc + x, yc - y, 6, sp, ep);
PositiveSectorPoint(xc + y, yc - x, 7, sp, ep);
if (d + y > 0) {
y = y - 1;
d = d - 2 * y + 1;
}
else {
if (x > d) {
x = x + 1;
d = d + 2 * x + 1;
}
}
}
}
//=================================================================
//PositiveSectorPoint
//Point plotting routine for the Positive direction arc sections
// Inputs
// x,y point to plot
// s sector to check
// sp, ep StartX Point and EndX Point
//=================================================================
void PositiveSectorPoint (int x, int y, int s, int sp, int ep)
{
if (arc_sector[s] == NOT_DRAWN) return;
if (arc_sector[s] == ALL_DRAWN) { //draw all points of this sector
pixel (x, y); return; }
if (arc_sector[s] == STARTS_HERE) { //draw all points flowing to right
if (x >=sp) { pixel (x, y); return; }
}
if (arc_sector[s] == ENDS_HERE) { //draw all points flowing from left
if (x <= ep) {pixel (x, y); return; } } if (arc_sector[s] == STARTS_ENDS_HERE) { //fill only sections of this sector. if ((x >= sp) && (x <= ep)) pixel (x, y);
}
}
//=================================================================
//NegativeSectorPoint
//Point plotting routine for the Negative direction arc sections
//
// Inputs
// x,y point to plot
// s sector to check
// sp, ep StartX Point and EndX Point
//=================================================================
void NegativeSectorPoint (int x, int y, int s, int sp, int ep)
{
if (arc_sector[s] == NOT_DRAWN) return;
if (arc_sector[s] == ALL_DRAWN) { //Draw all points in this sector
pixel(x, y); return; }
if (arc_sector[s] == STARTS_HERE) { //Draw all points flowing to the left
if (x <= sp) {pixel (x, y); return; } } if (arc_sector[s] == ENDS_HERE) { //Draw all points flowing from the right if (x >= ep) {pixel (x, y); return; }
}
if (arc_sector[s] == STARTS_ENDS_HERE) { //fill only sections of this sector.
if ((x >= ep) && (x <= sp)) pixel (x, y);
}
}
SOLID CIRCLE - Algorithm
//
//Draw a solid circle
//
void CircleScans(xc, yc, x, y)
int xc, yc, x, y;
{
line(xc+x, yc+y, xc-x, yc+y);
line(xc+y, yc+x, xc-y, yc+x);
line(xc+y, yc-x, xc-y, yc-x);
line(xc+x, yc-y, xc-x, yc-y);
}
void SolidCircle(int xc, int yc, int r)
{
int x,y,d;
x = 0;
y = r;
d = 2*(1-r);
while (y>=x {
CircleScans(xc, yc, x, y);
if (d+y>0) {
y=y-1;
d=d-2*y+1;
}
if (x>d) {
x=x+1;
d=d+2*x+1;
}
}
}
void main()
{
SolidCircle(random(500)+50,random(350)+25,Radius);
}
SOLID ARC - Algorithm
int Start_Angle = 30;
int End_Angle = 200;
int Arc_CX;
int Arc_CY;
#define Radius 150
#define NOT_DRAWN 0
#define STARTS_HERE 1
#define ALL_DRAWN 2
#define ENDS_HERE 3
#define STARTS_ENDS_HERE 4
#define R_TO_D 57.29578
int arc_sector[8];
void pixel(int x, int y)
{
line(x,440-y, Arc_CX, 440-Arc_CY);
}
void PositiveSectorPoint (int x, int y, int s, int ss, int es)
{
if (arc_sector[s] == NOT_DRAWN) return;
if (arc_sector[s] == ALL_DRAWN) {
pixel (x, y);
}
if (arc_sector[s] == STARTS_HERE) {
if (x >=ss) pixel (x, y);
}
if (arc_sector[s] == ENDS_HERE) {
if (x <= es) pixel (x, y); } if (arc_sector[s] == STARTS_ENDS_HERE) { if ((x >= ss) && (x <= es)) pixel (x, y);
}
}
void NegativeSectorPoint (int x, int y, int s, int ss, int es)
{
if (arc_sector[s] == NOT_DRAWN) return;
if (arc_sector[s] == ALL_DRAWN) { pixel(x, y); }
if (arc_sector[s] == STARTS_HERE) {
if (x <= ss) pixel (x, y); } if (arc_sector[s] == ENDS_HERE) { if (x >= es) pixel (x, y);
}
if (arc_sector[s] == STARTS_ENDS_HERE) {
if ((x >= es) && (x <= ss)) pixel (x, y);
}
}
void SolidCurve (int xc, int yc, int r, int sa, int ea)
{
int start_sector,end_sector;
int i;
int x,y;
float rd;
float sang,eang;
int es,ss,d;
Arc_CX=xc;
Arc_CY=yc;
for (i= 0; i< 8; i++) { arc_sector[i] = 0; }
start_sector = sa / 45;
end_sector = ea / 45;
if (start_sector == end_sector) {
arc_sector[start_sector] = 4;
}else {
for (i = start_sector; i< end_sector; i++) arc_sector[i] = 2; arc_sector[start_sector] = 1; arc_sector[end_sector] = 3; } /*''Calculate the Start and End Points*/ /*''Calculate points in first sector and translate*/ x = 0; y = r; rd = 3.14 / 180; sang = sa; /*((sa) * rd);*/ eang = ea; /*((ea) * rd);*/ ss = ((double)xc + (double)r * cos((double)sang/R_TO_D)); es = ((double)xc + (double)r * cos((double)eang/R_TO_D)); /* setcolor(RED); line (ss,0,ss,439); setcolor(CYAN); line (es,0,es,439); */ d = 2 * (1 - r); while (y >= x)
{
NegativeSectorPoint(xc + y, yc + x, 0, ss, es);
NegativeSectorPoint(xc + x, yc + y, 1, ss, es);
NegativeSectorPoint(xc - x, yc + y, 2, ss, es);
NegativeSectorPoint(xc - y, yc + x, 3, ss, es);
PositiveSectorPoint(xc - y, yc - x, 4, ss, es);
PositiveSectorPoint(xc - x, yc - y, 5, ss, es);
PositiveSectorPoint(xc + x, yc - y, 6, ss, es);
PositiveSectorPoint(xc + y, yc - x, 7, ss, es);
if (d + y > 0) {
y = y - 1;
d = d - 2 * y + 1;
}
else
{
if (x > d) {
x = x + 1;
d = d + 2 * x + 1;
}
}
}
}
void main()
{
Curve(200,220, Radius, Start_Angle, End_Angle);
}
More
In case you missed it – read our post on Fast Line Drawing Routines
Partner Advertising